oregonhasem.blogg.se - Hangman python 2.7.9 2 player

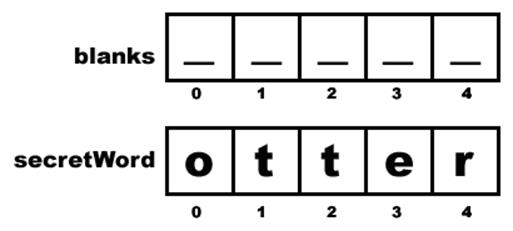
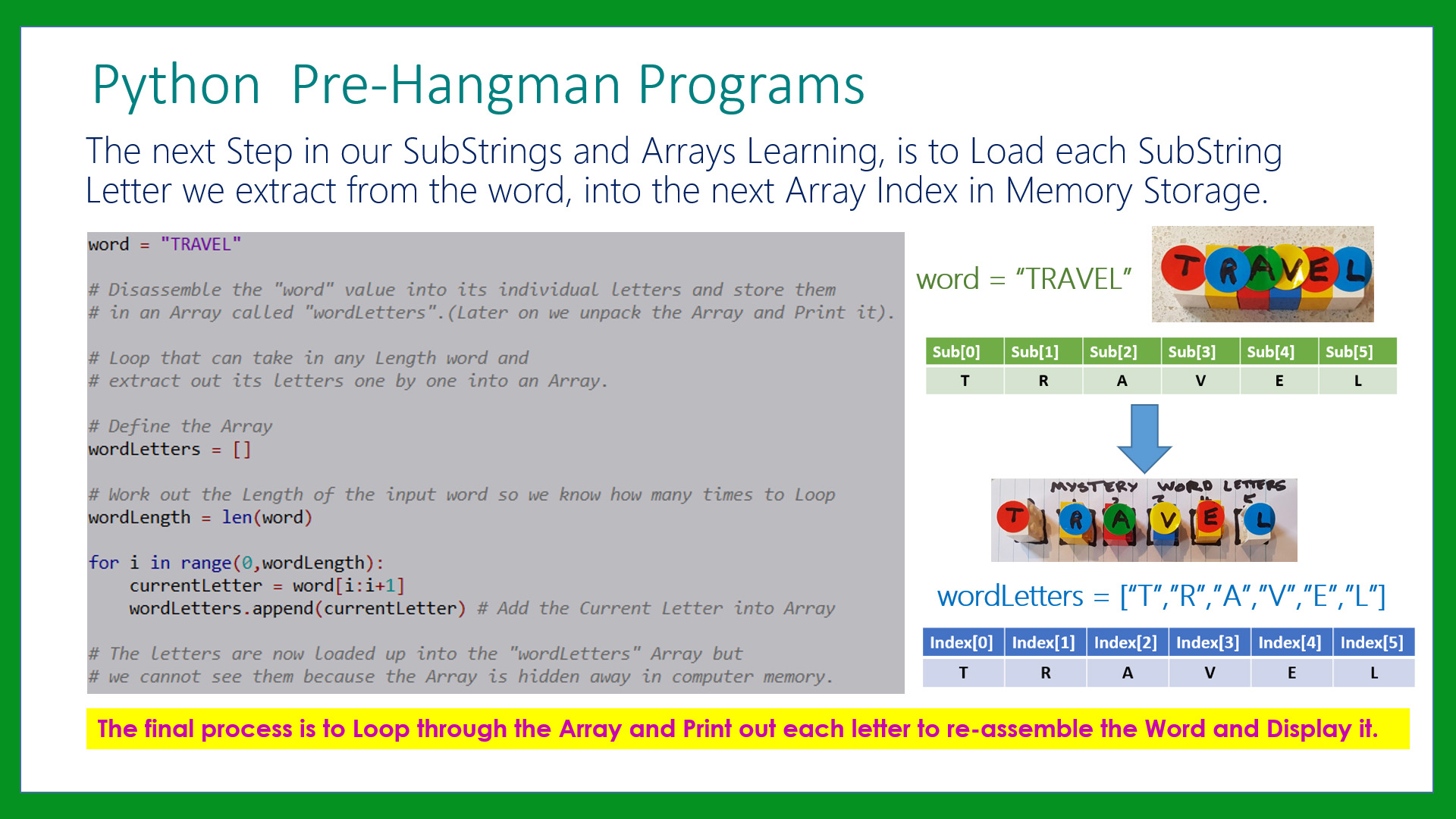
Play(image, currentImg, misses, word, blanks, used) Misses, currentImg, word, blanks, used = reset(image, wordlist) Print("Guess the word before the man is hung and you win!")

Print "Nice try! Your word was '%s'." % word Print "You correctly guessed the word '%s'!" % word

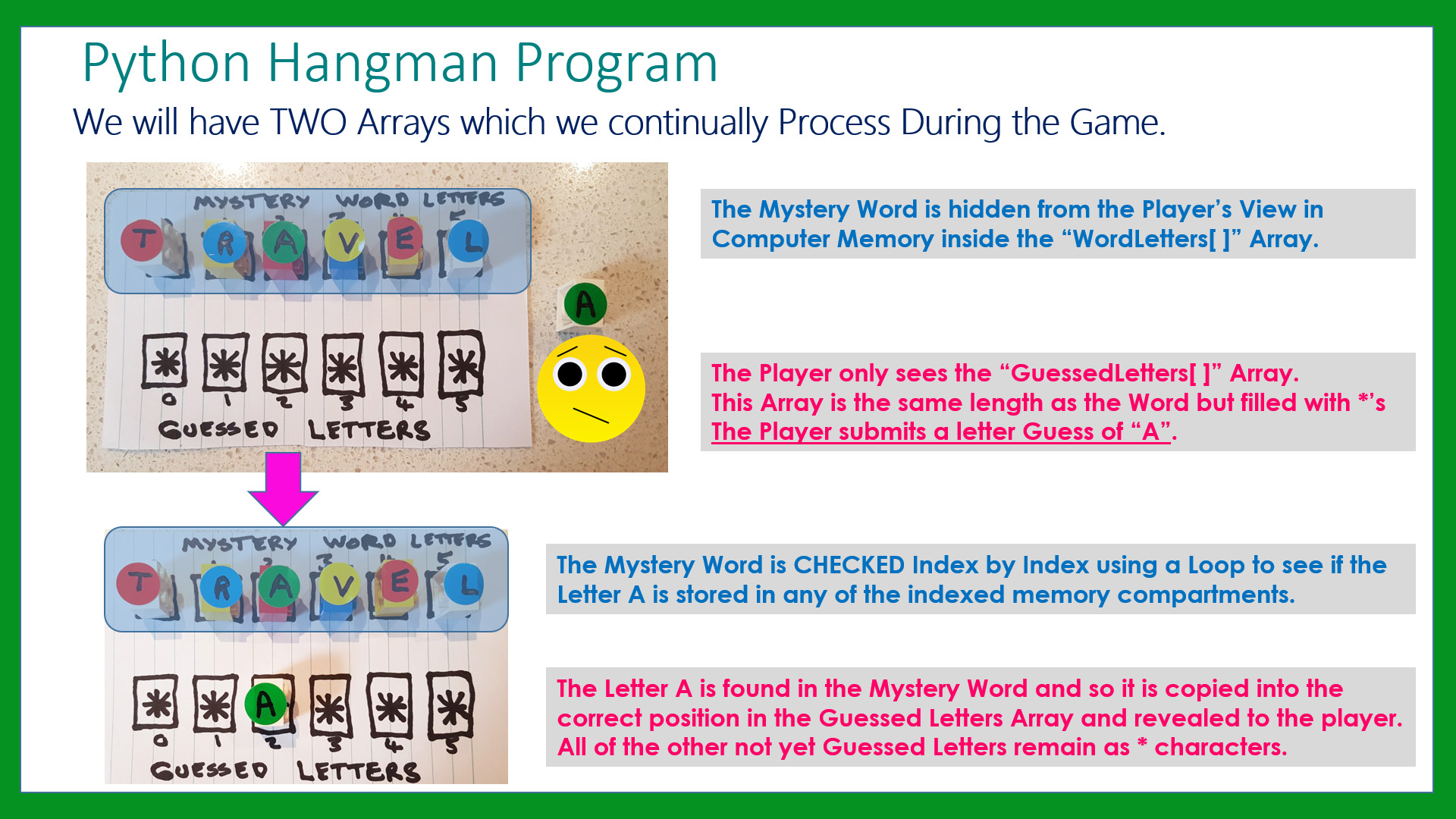
Play(image, currentImg, wrongGuesses, word, blanks, used)Įlif missed = False and blanks != list(word) and wrongGuesses != 7: Return wrongGuesses, currentImg, word, blanks, usedĭef play(image, currentImg, wrongGuesses, word, blanks, used):īlanks, used, missed = check_letter(word, guess.lower(), blanks, used, missed)ĬurrentImg = t_state(wrongGuesses) Word = wordlist.new_word() # word to be guessedīlanks = set_blanks(word) # blanks which hide each letter of the word until guessed WrongGuesses = 0 # number of incorrect guessesĬurrentImg = t_state(wrongGuesses) # current state of the gallows Os.system('cls' if os.name = 'nt' else 'clear') Used += guess # add the guess to the used letter list NewWord = newWord.replace(guess, '-', 1) # replace already checked letters with dashes # replace the corresponding blank for each instance of guess in the word Raw_input("You already tried that letter, silly!") # If the user inputs a letter they've already used

Raw_input("You can't guess more than one letter at a time, silly!") # If the user inputs multiple letters at once Raw_input("You have to guess a letter, silly!") # If the user presses enter without entering a letter '''Check if guessed letter is in the word.''' '''Create blanks for each letter in the word.'''ĭef check_letter(word, guess, blanks, used, missed): Word = line.lower().strip() # remove endline characters StopNum = random.randint(0, self.numLines-1) # establish random number to be picked from list Self.numLines = sum(1 for line in open('test.txt')) # construct gallows image into str from list State = self.state # set state to the list of desired gallows image '''Sets the current visual being used.''' Raw_input('This program requires Python 2.x to run.') Note that every solution is reachable with at most three incorrect guesses.To learn Python, I've been working through Learn Python the Hard Way, and to exercise my Python skills I wrote a little Python Hangman game (PyHangman - creative, right?): #! /usr/bin/env python2.7 Green rightward lines lead to possible outcomes for matching guesses, and red downward lines are taken when there's no match. Italicized numbers represent blanks that have only one possible way to fill them. Here's a flowchart representation of the guessing strategy, with all possible solutions to the $\_ + \_ = \_$ problem: There's no way to guarantee a win with 3 tokens, because there's no set of three digits such that every possible solution contains at least one digit from the set. There are some variations possible (for example, $3$ can be guessed before $1$, or the follow-up guesses after a $3$ match could be $4$, $5$, $6$). But the problem must contain $4$, so we can guess that, which will reveal the solution (either $4 + 4 = 8$ or $4 + 5 = 9$).

If the first three guesses were all misses, we're down to our last token.

If it's a match, but the solution is still ambiguous, the problem must contain $6$ or $7$, so those can be guessed in order, losing at most one additional token (for three lost total).

If the first two guesses were misses, guess $2$.

If it's a match, but the solution is still ambiguous, the problem must contain a $5$, $7$, or $9$, so those can be guessed in order, losing at most two additional tokens (for three lost total).

If the first guess was a miss, guess $3$.

If it's a match, but the solution is still ambiguous, the problem must contain a $3$, $5$, $7$, or $9$ so those can be guessed in order, losing at most three tokens. The Guesser can guarantee a win with 4 tokens. He writes the addition $x+y=z$ in base $10$, replaces each digit by a blank space ($\underline$ The first player (the Chooser) chooses an addition problem $x+y=z$, where $x$, $y$, and $z$ are positive integers. Addition Hangman is a game for two players.